Detection of Gravitational Waves using Deep Learning
Ground-based interferometers now routinely detect gravitational waves (GWs) from compact binary coalescences (CBCs). While most detections so far are binary black hole (BBH) mergers, a few binary neutron star (BNS) and neutron star–black hole (NSBH) events have also been observed. The first BNS event, GW170817, ushered in multi-messenger astronomy and enabled key measurements of the Hubble constant and neutron-star physics. As detector sensitivity improves and new instruments come online, the prospect of more multi-messenger detections motivates development of complementary CBC search methods.
Current CBC searches rely on matched-filtering pipelines, which correlate data against banks of signal templates. These pipelines are effective but still face challenges from non-Gaussian noise transients (“glitches”) and long-duration BNS signals. Deep learning offers an alternative: by training neural networks to recognize signal features, it may be possible to detect CBCs with comparable sensitivity, reduced latency, and greater robustness to glitches.
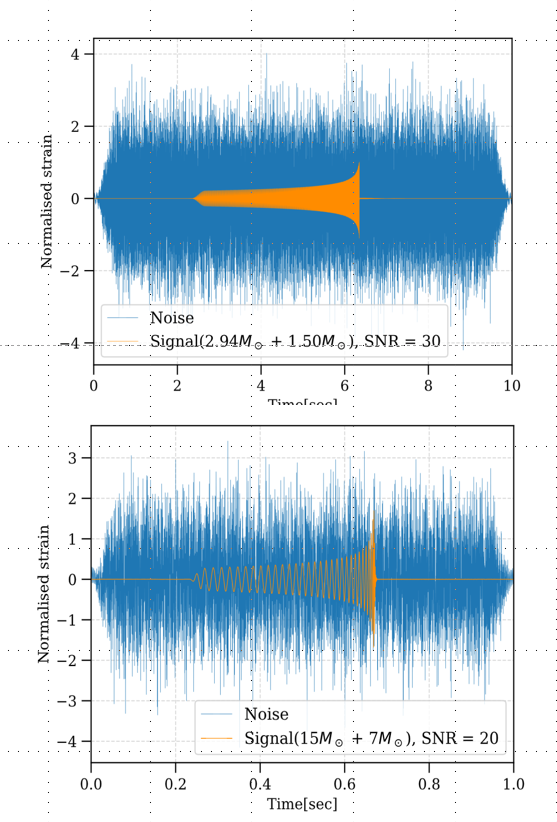
In this work, we explore a neural network pipeline that ingests the signal-to-noise ratio (SNR) time series produced by matched filtering. Using SNR series condenses CBC power into shorter time windows, making it especially promising for longer BNS signals and straightforward to integrate with existing search products.
- Approach: We train convolutional and residual neural networks on matched-filtering SNR series for both BBH and BNS signals. We compare traditional “pre-computed” data augmentation with an efficient “on-the-fly” method.
- Key Findings:
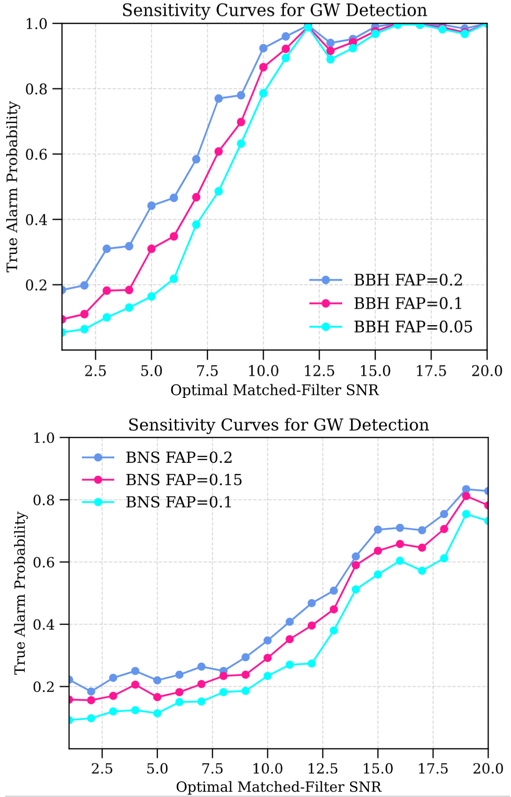
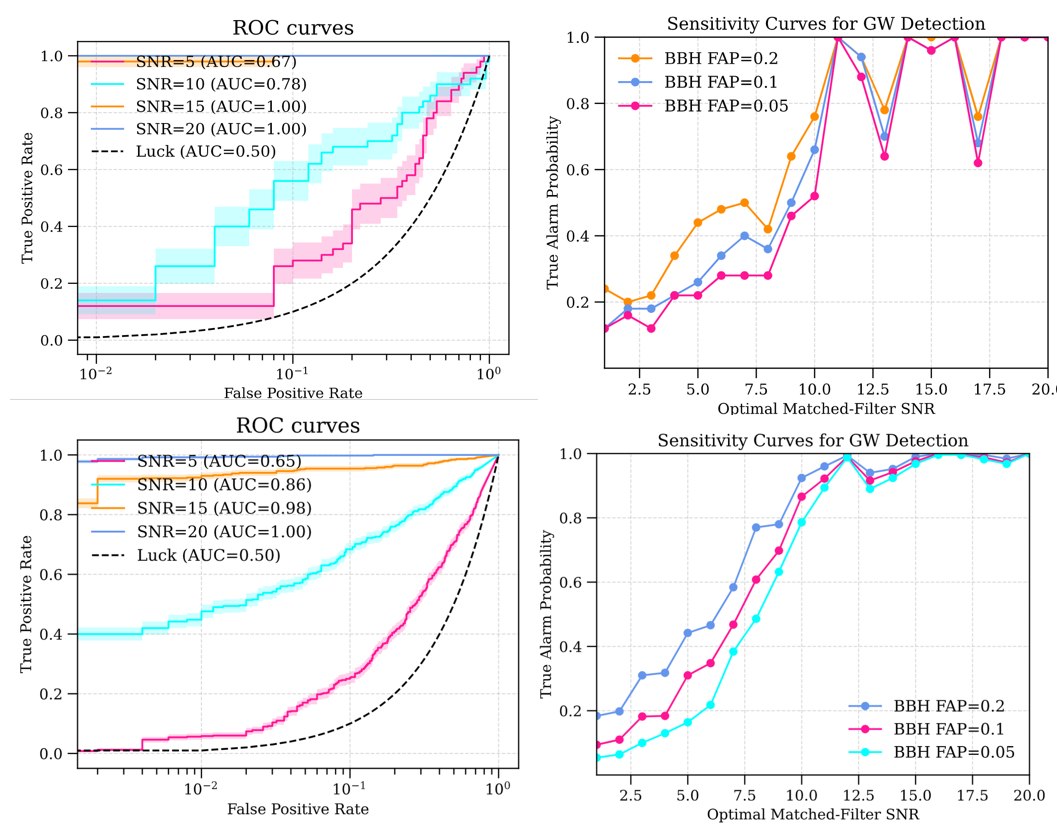
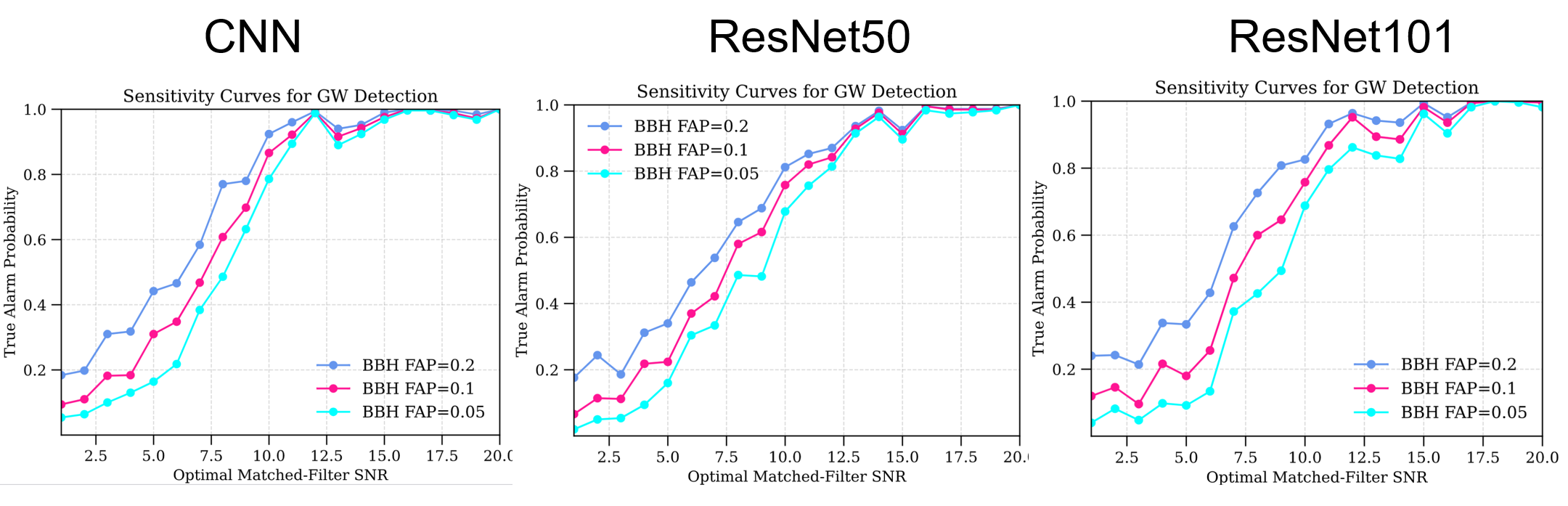
- Sensitivity: Neural networks reach competitive sensitivity for BBH signals, with deeper residual models (e.g., ResNet101) outperforming simpler CNNs.
- BNS Challenges: Detecting long-duration BNS signals remains harder, likely due to dataset size and waveform complexity.
- Data Augmentation: On-the-fly augmentation converges faster and requires far less storage, with only minor loss in sensitivity.
- Outlook: To further improve BNS detection, future work should expand and diversify training data—ideally incorporating real interferometer noise—and explore architectures or feature-extraction strategies tailored to BNS waveforms. Balancing model complexity and real-time performance will be crucial for deployment in next-generation search pipelines.
This study demonstrates that deep learning on matched-filtering outputs holds promise as a complementary CBC detection method, particularly for BBH signals, and offers a roadmap for overcoming challenges in BNS detection and real-time application.
Availability